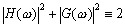 (1.2)
(1.2)
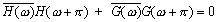
Разложение по поддаипазонам
Мы хотим найти два фильтра, h (подавляющий высокие частоты) и g
(подавляющий низкие частоты), которые позволяли бы разложить сигнал на
две компоненты, ![]() и
и ![]() , вдвое
их проредить (половина значений становится лишней – ведь частотный диапазон
сократился вдвое!), а затем, с помощью транспонированных фильтров, точно
восстановить по этим данным исходный сигнал (эту операцию можно
применять рекурсивно). Условия на искомые фильтры удобно записать в терминах
z-преобразования.
, вдвое
их проредить (половина значений становится лишней – ведь частотный диапазон
сократился вдвое!), а затем, с помощью транспонированных фильтров, точно
восстановить по этим данным исходный сигнал (эту операцию можно
применять рекурсивно). Условия на искомые фильтры удобно записать в терминах
z-преобразования.
Пусть ![]() –
z-преобразование одной из компонент. Перед кодированием она
прореживается вдвое, а перед восстановлением исходного сигнала доводится до
исходной длины вставкой нулей между соседними значениями. При этом z-преобразование
из
–
z-преобразование одной из компонент. Перед кодированием она
прореживается вдвое, а перед восстановлением исходного сигнала доводится до
исходной длины вставкой нулей между соседними значениями. При этом z-преобразование
из ![]() превращается в
превращается в ![]() .
Подставим сюда (1.1’) для каждого из фильтров, и получим z-преобразования
компонент перед восстановлением
.
Подставим сюда (1.1’) для каждого из фильтров, и получим z-преобразования
компонент перед восстановлением
z-преобразования транспонированных фильтров имеют вид ![]() и
и ![]() . Сигнал
восстановится с их помощью точно, если:
. Сигнал
восстановится с их помощью точно, если:
Получаем условия точного восстановления (perfect reconstruction, PR):
В матричной форме они записываются так: ![]()
где
Подставив ![]() , получим
условия на ДПФ искомых фильтров:
, получим
условия на ДПФ искомых фильтров:
Допустим, что мы нашли h такой, что
(1.2’)
Тогда, положив
(1.3)
мы видим, что (1.2) выполняется. Задача свелась к нахождению
тригонометрического многочлена ![]() ,
удовлетворяющего (1.2’). На методах построения таких многочленов мы
остановимся в следующей лекции. Фильтры h и g, удовлетворяющие
(1.2), называются квадратурными зеркальными фильтрами (quadrature mirror
filters, QMF).
,
удовлетворяющего (1.2’). На методах построения таких многочленов мы
остановимся в следующей лекции. Фильтры h и g, удовлетворяющие
(1.2), называются квадратурными зеркальными фильтрами (quadrature mirror
filters, QMF).
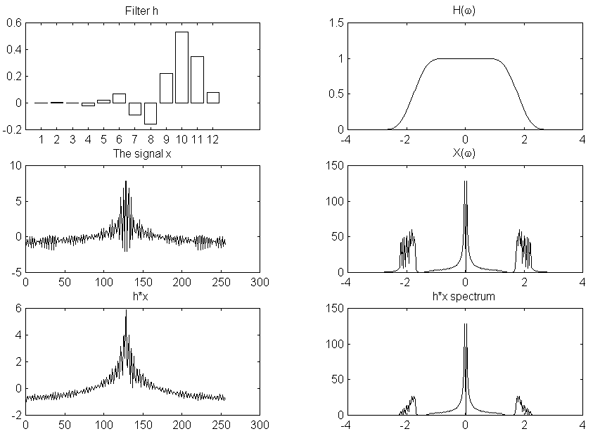
На рис.1, (a) и (b), показаны ДПФ такой пары фильтров h и g, а также исходный сигнал до и после фильтрации (без прореживания).
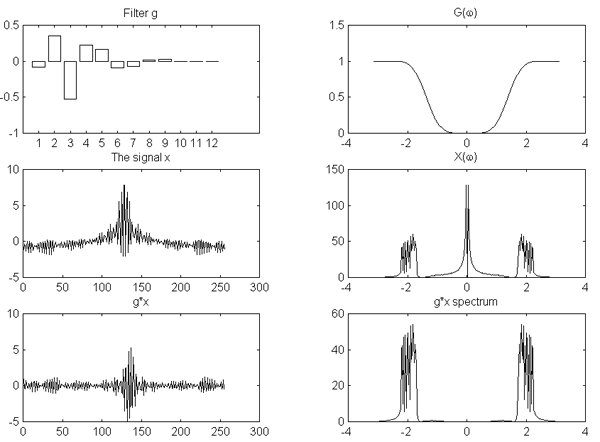
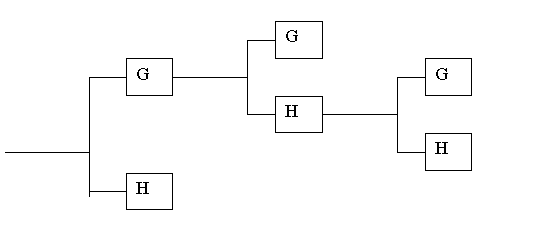
Точно такую же операцию можно применить к одной или обеим из полученных компонент, и т.д., добиваясь нужной локализации по частоте. Это позволяет адаптироваться к особенностям сигнала за счет выбора подходящего “дерева разложения”. Оно может выглядеть, например, так: